Page 127 - 2024年第55卷第7期

０．１，以此反映不同稳健程度的水资源优化配置结果，供决策者基于风险偏好进行决策。
表 １ 行业用水排污系数

用水行业 生活 工业 农业 第三产业
排放系数 ［ ０．３１５，０．３８５］ ［０．０９９，０．１２１］ ［０．４１４，０．５０６］ ［０．３１５，０．３８５］

表 ２ 行业用水效益系数 单位：元?ｍ ３
工业 农业 生活 生态
荆门市 ［ ３．３１，４．０５］ ［７．５３，９．２０］ ［１０．７３，１３．１１］ ［１０．７３，１３．１１］
潜江市 ［ ３．７７，４．６１］ ［７．６８，９．３８］ ［１３．００，１５．８９］ ［１３．００，１５．８９］
神农架林区 ［ ３．６１，４．４１］ ［３４．９０，４２．６５］ ［８．３４，１０．２０］ ［８．３４，１０．２０］
十堰市 ［ ５．６７，６．９３］ ［２２．０９，２７．００］ ［９．５５，１１．６７］ ［９．５５，１１．６７］
天门市 ［ ４．００，４．８９］ ［５．５３，６．７５］ ［６．４１，７．８３］ ［６．４１，７．８３］
武汉市 ［ ７．１４，８．７２］ ［１９．４２，２３．７３］ ［２６．５６，３２．４７］ ［２６．５６，３２．４７］
仙桃市 ［４．０３，４．９３］ ［６．３０，７．７０］ ［８．６６，１０．５８］ ［８．６６，１０．５８］
襄阳市 ［２．８８，３．５２］ ［１２．０５，１４．７２］ ［１３．６５，１６．６８］ ［１３．６５，１６．６８］
孝感市 ［１．７４，２．１２］ ［８．９５，１０．９３］ ［７．６３，９．３２］ ［７．６３，９．３２］
南阳市 ［ ７．３０，８．９３］ ［２１．９９，２６．８７］ ［９．０１，１１．０１］ ［９．０１，１１．０１］

３．３ 模型结果及讨论 水质保护与用水效率的主从
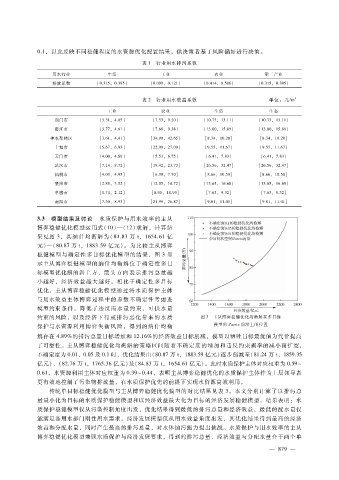
博弈稳健优化模型运用式（１０）—（１２）求解，计算结
果见图 ３，其纳什均衡解为 （８４．８３万 ｔ，１６５４．６１亿
元）—（８０．８７万 ｔ，１８８３．５９亿元）。为比较主从博弈
稳健模型与确定性多目标优化模型的结果，图 ３显
示主从博弈稳健模型的纳什均衡解位于确定性多目
标模型优化解的斜上方，箭头方向表示排污总量越
小越好，经济效益越大越好。相比于确定性多目标
优化，主从博弈稳健优化模型通过将水质保护主体
与用水效益主体博弈过程中的参数不确定性考虑进
模型约束条件，降低了违反需水量约束、可供水量
约束的风险，以及经济下行或排污恶化带来的水质 图 ３ 主从博弈稳健优化均衡解在多目标
保护与水资源利用博弈失衡风险，得到的纳什均衡 模型的 Ｐａｒｅｔｏ前沿上的位置
解存在 ４．８９％的排污总量目标增加和 １２．１６％的经济效益目标削减，模型以牺牲目标最优值为代价提高
了可靠性。主从博弈稳健优化均衡解的策略区间随着不确定度的增加和违反约束概率的减小而扩宽，
不确定度为 ０．０１、０．０５及 ０．１时，优化结果由（８０．８７万 ｔ，１８８３．５９亿元）逐步削减至（８１．２４万 ｔ，１８５９．３５
亿元）、（８２．７６万 ｔ，１７６５．３６亿元）及（８４．８３万 ｔ，１６５４．６１亿元）。此时水质保护主体对应权重为 ０．５９～
０．６１ ，水资源利用主体对应权重为 ０．３９～０．４４，表明主从博弈稳健优化的水质保护主体作为上层领导者
更有效地控制了污染物排放量，在水质保护优先的前提下实现水资源高效利用。
传统单目标稳健优化模型与主从博弈稳健优化模型的对比结果见表 ３，本文分别计算了以排污总
量最小化为目标的水质保护稳健模型和以经济效益最大化为目标的经济发展稳健模型。结果表明：水
质保护稳健模型仅从污染控制角度出发，优化结果得到最低的排污总量和经济效益，最低的配水量仅
能满足各用水部门刚性用水需求。经济发展模型仅从用水效益角度出发，其优化结果得到最高的经济
效益和分配水量，同时产生最高的排污总量，对水体纳污能力提出挑战。水质保护与用水效率的主从
博弈稳健优化模型兼顾水质保护与经济发展要求，得到的排污总量、经济效益与分配水量介于两个单

— ８ ７ ９ —