Page 99 - 2024年第55卷第10期

计算得到 α ＝ ０．８１＞０．８０，说明各变量间的计算维度均表现出了较高的平稳性，问卷数据拥有较好的信
度，达到实证的需求，因此问卷调查结果可以接受。
通过对问卷数据进行 ＫＭＯ和巴特利特检验数据有效性，判断样本数据是否均发挥了重要作用。
一般 ＫＭＯ值大于 ０．６０，则认为适合做探索性因子分析。问卷数据的 ＫＭＯ和巴特利特检验，ＫＭＯ为
０．６５＞０．６０，表明问卷的每个问题都是有效的，均发挥了一定的重要性。
由上所述，本文调查问卷的数据可信度和有效度较为理想。
依据本文所设风险方案，结合各模式打分结果，通过集值统计法 ［２８］ 对模糊与随机的风险指标展开
区间化描述，计算单源风险方案概率估计值；将各模式概率分值作为输入数据，利用变异系数定义推
论建立的耦合度模型 ［２９］ 即式（８），求解多源风险方案概率估计值。
ｍｉｎ（Ｐ，Ｐ）
１
２
(
Ｐ ＝ ( １ － （Ｐ－ Ｐ）) × ｍａｘ（Ｐ，Ｐ） ) ｔ × τ （８）
２
槡
１
２
２
１
式中：Ｐ为多源风险耦合概率值；Ｐ、Ｐ为不同源风险模式的概率值；ｔ为调节系数；τ 为折减系数。
２
１
５．２ 供水风险损失 针对风险方案的损失严重度估计，结合 《水资源短缺风险管理理论图与实践》 ［３０］
的研究内 容，使用 张芸 霞 ［３１］ 提 出的 风险率 （Ｒｉｓｋｒａｔｅ，Ｒ ）、脆 弱性 （Ｖｕｌｎｅｒａｂｉｌｉｔｙ，Ｖ ）、可 恢 复 性
１ １
（ Ｒｅｃｏｖｅｒａｂｉｌｉｔｙ，Ｒ）、重现期（Ｒｅｐｒｏｌａｐｓｅｐｅｒｉｏｄ，Ｒ）和风险度（Ｒｉｓｋｄｅｇｒｅｅ，Ｒ）五个风险指标，简称
３
２
４
４Ｒ１Ｖ供水风险指标体系，采用可变模糊综合评判模型 ［３２］ 对 Ｓ—Ｓ 各方案供水风险严重度等级进行估
１ １２
计，构造相对隶属度矩阵求得权重，并对 ４Ｒ１Ｖ指标值进行计算，其中 Ｒ、Ｖ、Ｒ 是越小越优型指
１ １ ４
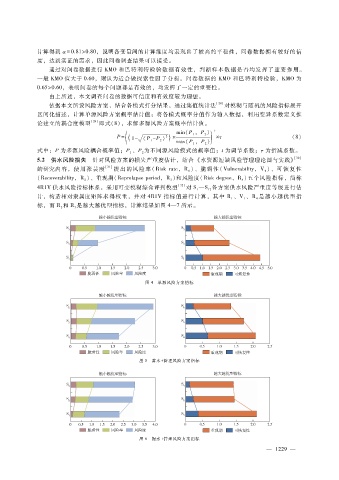
标，而 Ｒ和 Ｒ是越大越优型指标，计算结果如图 ４—７所示。
３
２

图 ４ 单源风险方案指标

图 ５ 蓄水＋ 管理风险方案指标

图 ６ 提水＋ 管理风险方案指标
２
— １ ２ ９ —