Page 76 - 2024年第55卷第12期

水流挟沙力的变化规律和计算方法值得更进一步的研究。黄河下游作为著名多沙河流，拥有长时间序
列水文资料，且床沙悬沙粒径均小于一般河流，以悬沙输移为主 ［１０］ 。故本文利用黄河实测资料检验西
方及受其影响的水流挟沙力公式精度，剖析影响水流挟沙力公式精度的内在因素。

２ 水流挟沙力公式检验

２．１ 水沙验证资料 本文收集 １９６０—１９９５年黄河下游花园口、夹河滩、高村、孙口、艾山、泺口和
利津共 ７个水文站实测水文资料，以及黄河中上游龙门、潼关、洛惠渠、渭河华县、毛不拉沟、裴峪
和三门峡等 ７个水文站实测水文资料。由于黄河下游冲积河流符合典型的河床和水流自动调整作用，
并符合 “趋衡原理” ［１１］ ，水文站实测含沙量基本应自然分布在冲淤平衡状况下的含沙量（即水流挟沙
力）周围，因此无需设置标准人为甄别是否冲淤平衡。
３
水文数据集的 １４００组验证样本部分参数如下：流量 Ｑ变化范围 ０．５４～１４６００ｍ ?ｓ；含沙量 Ｓ变化
３
范围 ０．１３９～１１２０ｋｇ?ｍ ；水面比降 Ｊ变化范围 ０．０６７  ～９ ；床沙中径 Ｄ 为 ０．０１１６～０．５ｍｍ。本文对
５０
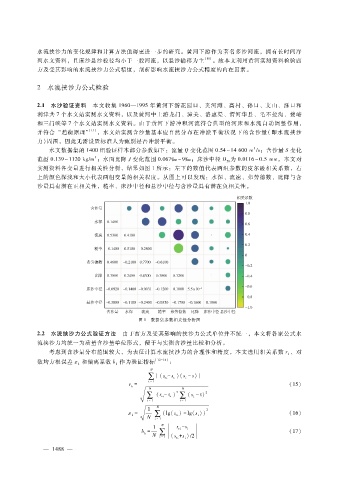
实测资料各变量进行相关性分析，结果如图 １所示：左下的数值代表两组参数的皮尔逊相关系数，右
上的颜色深浅和大小代表两组变量的相关程度。从图上可以发现：水深、流速、弗劳德数、比降与含
沙量具有潜在正相关性，糙率、床沙中径和悬沙中径与含沙量具有潜在负相关性。

图 １ 数据集参数相关性分析图

２．２ 水流挟沙力公式验证方法 由于西方及受其影响的挟沙力公式单位并不统一，本文将各家公式水
流挟沙力均统一为质量含沙量单位形式，便于与实测含沙量比较和分析。
考虑到含沙量分布范围较大，为表征计算水流挟沙力的合理性和精度，本文选用相关系数 ｒ、对
ｋ
和偏离系数 ｂ 作为验证指标 ［１２ － １４］ ：
数均方根误差 ε ｋ
ｋ
Ｎ
∑ ［（ｓ － 珋 ｉ ｓ）］
ｓ）（ｓ － 珋
 ｉ 
ｉ ＝１
ｒ＝ （１５）
ｋ
Ｎ ２ Ｎ ２
 ｉ  ∑
ｓ
∑
ｓ）
槡 （ ｓ － 珋 ） ｉ ＝１ （ｓ － 珋
ｉ
ｉ ＝１
１ Ｎ ２
＝ ∑ （ｌｇ（ｓ） － ｌｇ（ｓ）） （１６）
槡
ε ｋ  ｉ ｉ
Ｎ ｉ ＝１
１ Ｎ ｓ－ ｓ
ｉ
 ｉ
ｂ＝ ∑ （１７）
ｋ
Ｎ ｉ ＝１ （ｓ＋ ｓ）?２
 ｉ ｉ
— １ ４ ８ —
８