Page 94 - 2025年第56卷第11期

分布：用于处理时间序列尾部的偏斜现象，具体表达式如下：
ì r i，t = φ 0 + φ 1 r × r + … + φ p r i，p × r i，t - p + θ 1 α × ε + … + θ q α i，t - q × ε i，t - q + ε i，t
ï ï i，1 i，t - 1 i，1 i，t - 1
ï
ï ε i，t = σ i，t × μ i，t
ï ï
í ) （3）
μ
ï ï σ 2 = ω i + α × ε 2 + β × σ 2
~skewed - t( skew i ，shape i
ï
i，t
ï
ï ï
î
i，t
i，t
i，t - 1
i，t - 1
i，1
式中：r 为各延迟流序列，在对 r 进行边缘分布建模时，采用 ARMA（p，q）模型进行拟合，模型参数

i，t
i，t
为 φ ，φ ，⋯，φ 和 θ ，⋯，θ ；ε 表示残差，σ 表示时刻 t 的条件方差，μ 为偏态 τ 分布的位移参
0 1 p 1 q i，t i，t i，t
数；残差项服从 skewed-t 分布，该分布在传统 t 分布的基础上引入了偏度参数 （skew），使其在均值两侧
的尾部厚度呈现不对称性，从而能够更准确地反映径流序列的正偏或负偏特征，其中，参数 skew 和
i
shape 分别用于描述分布的偏度与峰度；ω 、α 和 β i，1 为 GARCH（1，1）模型的参数。该设定能够同时反
i
i
i，t
映延迟流的线性依赖结构、条件异方差特征及分布形态特征，为后续边缘分布与联合分布的构建提供
坚实基础。
（3）从拟合的 ARMA（p，q）-GARCH（1，1）-τ 模型中提取残差和条件方差。为消除波动性影响，
将残差除以对应的条件方差，得到标准化残差。为验证 ARMA（p，q）-GARCH（1，1）-τ 模型是否成功
消除自回归条件异方差性和自相关性，需要对标准化残差及其平方项进行 Ljung-Box 检验和 ARCH-LM
检验。通过经验累积分布函数将标准化残差映射到［0，1］分布区间，满足 Copula 模型对边缘分布均匀
性的要求。转化后的相对位置值作为 Copula 模型的输入，用于构建多变量间的联合分布。
（4）Vine Copula 是一种将高维联合分布分解为一系列二元 Copula 函数的多元结构化建模工具。本
文基于 4 个延迟流组分构建四维藤结构，该结构由 3 层树组成，共包含 9 个节点，节点代表延迟流变量
或条件变量。节点由六条边连接。每条边对应一个 Copula 函数，用于描述两个延迟流变量或条件变量
之间的相关性。本研究应用赤池信息准则（Akaike Information Criterion， AIC）对 6 个 Copula 函数进行评
估和选择，并以 AIC 值最小者作为最优 Vine Copula 结构。此外，每个二元 Copula 函数的参数根据 Ken‐
dall′s tau 与 Copula 参数之间的关系确定，公式如下：
2
τ = ∑ sign ( x i - x j ) × sgn ( y i - y j ) （4）
n( n - 1 ) i < j
C
τ = 4 ∬ ( u，v) dC( u，v) - 1 （5）
式中：n 为延迟流时间序列的长度；C( u，v) 为二元 Copula 函数，u 和 v为时间序列的边缘分布；sgn（⋅）为
符号函数。
（5）根据选定的最佳 Vine Copula 结构及 Copula 函数参数的估计值，逐层构建条件分布。根据式（6）
和式（7），将边缘分布与 Copula 函数整合，计算四个延迟流的联合分布。其中，FDC 的横轴：超越概
率=1-G (q q q q b )，FDC 的纵轴：按降序排列的流量模拟值。
l，
i，
s，
C (u 1 ，u 2 ，u 3 )
C 13|2 (u 1 ，u 3 |u 2 ) = 12，23 （6）
C 2 (u 2 )
C (u 1 ，u 2 ，u 3 ，u 4 ) = C (u 1 ，u 2 ) × C (u 2 ，u 3 ) × C (u 3 ，u 4 ) × C 13|2 (u 1 ，u 3 |u 2 ) ×
1，2 2，3 3，4
C 24|3 (u 2 ，u 4 |u 3 ) × C 14|23 (u 1 ，u 4 |u 2 ，u 3 ) （7）
式中：u 1 、u 2 、u 3 和u 4 分别代表短、中、长和基线延
迟 流 的 随 机 变 量 通 过 边 缘 FDC 转 换 后 的 值 ， 值 域
为［0，1］。
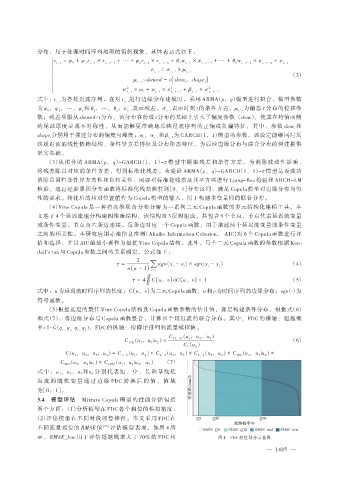
3.4 模型评估 Mixture Copula 模型的性能评估包括
两个方面：（1）分析模型在 FDC 各个相位的模拟精度；
（2）评估模型在不同时段的鲁棒性。本文采用 FDC 在
不同流量相位的 RMSE 值 ［23］ 评估模型表现。如图 4 所
示，RMSE_low 用于评估超越概率大于 70% 的 FDC 相 图 4 FDC 相位划分示意图

— 1485 —