Page 93 - 2025年第56卷第11期
P. 93
CDC 逐渐趋于平缓,表征从快速贡献向慢速贡献的转变 [11] 。当 N 值超过 60 d 时,CDC 斜率变化显著减
小,认为此时的流量足以代表最长延迟贡献的响应,故将 N max 设置为 60 d。
(3)在 CDC 中可识别出三个显著的转折点,从而定义出四类延迟流量:短延迟流(Q s ),中等延迟
-
流(Q i ),长延迟流(Q l )和基线延迟流(Q b )。其计算方式为:短延迟流 Q s = (DFI 0 - DFI BP1 ) × Q,代表从
无延迟到第一个转折点之间的流量,通常为响应最快的水源,如地表径流或瞬时地下径流贡献;中等
-
延迟流 Q i = (DFI BP1 - DFI BP2 ) × Q,代表第一个转折点到第二个转折点之间的流量,反映响应时间中等
-
的水源,如浅层地下径流或融雪贡献;长延迟流 Q l = (DFI BP2 - DFI 60 ) × Q,代表第二个转折点到 N =
-
60 d 的流量,主要来源于响应较慢的水源,如深层地下径流;基线延迟流 Q b = DFI 60 × Q,代表最慢的
水源贡献,通常与深层地下径流相关,在干旱期间维持河流的基流供给。
(4)鉴于基流仿真的准确性通常难以验证 [20] ,本
研 究 通 过 严 格 基 流 点 方 法 对 DFI 基 流 分 割 方 法 的 基
流 模 拟 效 果 进 行 评 估 。 严 格 基 流 点 方 法 在 我 国 流 域
的 研 究 中 已 被 证 实 具 有 可 靠 性 [21] 。 基 于 Xie 等 [22] 提
出 的 四 条 准 则 对 日 尺 度 流 量 实 测 序 列 进 行 筛 选 后 ,
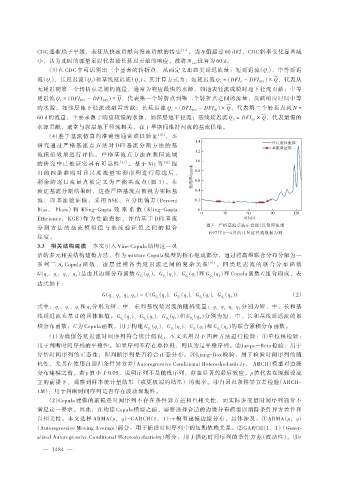
剩 余 的 逐 日 流 量 点 被 定 义 为 严 格 基 流 点(图 3)。 在
验证基流分割结果时,这些严格基流点被视为实际基
流,即基流验证值,采用 NSE、百分比偏差(Percent
Bias, Pbais)和 Kling-Gupta 效 率 系 数(Kling-Gupta
Efficiency, KGE)作 为 性 能 指 标 , 评 估 基 于 DFI 基 流
分 割 方 法 的 基 流 模 拟 值 与 基 流 验 证 值 之 间 的 拟 合 图 3 严格基流点法示意图(以旬河流域
1997 年 1—4 月的日尺度径流数据为例
程度。
3.3 相关结构建模 本文引入 Vine Copula 结构这一灵
活的多元相关结构建模方法,作为 mixture Copula 模型的核心组成部分,通过将高维联合分布分解为一
系 列 二 元 Copula 函 数 , 逐 层 建 模 各 类 延 迟 流 之 间 的 复 杂 关 系 [15] 。 四 类 延 迟 流 的 联 合 分 布 函 数
(q b ) 和 Copula 函数 C 组合而成,表
G (q s ,q i ,q l ,q b ) 是由其边缘分布函数 G Q s (q s )、G Q i (q i )、G Q l (q l ) 和 G Q b
达式如下:
s, i, l, (q b )) (2)
G (q q q q b ) = C (G Q s (q s ),G Q i (q i ),G Q l (q l ),G Q b
式中:q s 、q i 、q l 和 q b 分别为短、中、长和基线延迟流的随机变量;q q q q b 分别为短、中、长和基
s,
i,
l,
(q b ) 分别为短、中、长和基线延迟流的累
(q l ) 和 G Q b
(q i )、G Q l
线延迟流在某日的具体取值;G Q s
(q s )、G Q i
(q b )的联合累积分布函数。
积分布函数;C 为 Copula 函数,用于构建 G Q s (q s )、G Q i (q i )、G Q l (q l )和 G Q b
(1)为确保各延迟流时间序列符合统计假设,本文采用以下四种方法进行检验:①单位根检验:
用于判断时间序列的平稳性。如果序列不存在单位根,则认为是平稳序列。②Jarque-Bera 检验:用于
评估时间序列的正态性,即判断序列是否符合正态分布。③Ljung-Box 检验:用于检验时间序列的随
机性,尤其在使用自回归条件异方差(Autoregressive Conditional Heteroskedasticity, ARCH)模型对边缘
分布建模之前。若 p 值小于 0.05,说明序列不是随机序列,存在显著的滞后效应,p 值代表在原假设成
立的前提下,观察到样本统计量结果 (或更极端的结果) 的概率。④自回归条件异方差检验(ARCH-
LM):用于判断时间序列是否存在波动聚集性。
(2)Copula 建模的前提是时间序列不存在条件异方差和自相关性,而实际多变量时间序列通常不
满足这一要求。因此,在构建 Copula 模型之前,需要选择合适的边缘分布模型以消除条件异方差性和
自相关性。本文选择 ARMA(p,q)-GARCH(1,1)-τ 模型建模边缘分布,具体涉及:①ARMA(p,q)
(Autoregressive Moving Average)部分:用于捕捉时间序列中的短期依赖关系。②GARCH(1,1)(Gener‐
alized Autoregressive Conditional Heteroskedasticity)部分:用于描述时间序列的条件方差(波动性)。③τ
— 1484 —