Page 89 - 2022年第53卷第12期

元个数 Ｎ 。
ｍａｘ
（３）设置搜索横向分枝数 ｎ：在搜索失效路径的过程中，对每一个单元都进行横向分枝，才不会
ｂ
遗漏主要失效模式。这样操作效率较低，且横向分枝搜索出的大量失效路径形成的失效模式可能对整
个体系的可靠度贡献不大，往往可以忽略。引入横向分枝数 ｎ，可以提高失效模式搜索效率。对于重
ｂ
力坝而言，其静力工况下的失效路径往往是沿着薄弱环节发展的，可以近似地假设 ｎ＝ １ 。
ｂ
（ ４）在失效路径搜索过程中，以条件可靠指标 ［４１］ 最小原则确定下一失效单元；对于失效路径形成
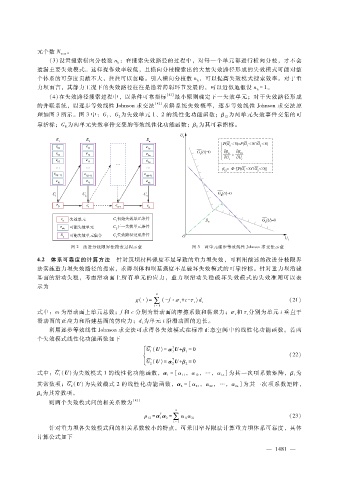
的并联系统，以逐步等效线性 Ｊｏｈｎｓｏｎ求交法 ［４２］ 求解系统失效概率，逐步等效线性 Ｊｏｈｎｓｏｎ求交法原
理如图 ３所示。图 ３中： 珔 Ｇ为失效单元 １、２的线性化功能函数；β １２ 为两单元失效事件交集的可
Ｇ、 珔
２
１
Ｇ 为其可靠指标。
靠指标； 珔 为两单元失效事件交集的等效线性化功能函数；β Ｅ
Ｅ

图 ２ 改进分枝限界法搜索过程示意 图 ３ 两单元逐步等效线性 Ｊｏｈｎｓｏｎ求交法示意
４．２ 体系可靠度的计算方法 针对筑坝材料强度不足导致的重力坝失效，可利用前述的改进分枝限界
法实施重力坝失效路径的搜索，求得坝体和坝基强度不足破坏失效模式的可靠指标。针对重力坝沿建
基面的滑动失稳，考虑滑动面上所有单元的应力，重力坝滑动失稳破坏失效模式的失效准则可以表
示为
ｍ
ｇ（·） ＝ ∑ （ － ｆ·σ ｉ ＋ ｃ － τ ｉ ）ｄ ｉ （２１）
ｉ ＝１
分别为单元 ｉ垂直于
式中：ｍ为滑动面上单元总数；ｆ和 ｃ分别为滑动面的摩擦系数和黏聚力；σ ｉ 和 τ ｉ
滑动面的正应力和沿建基面的剪应力；ｄ为单元 ｉ沿滑动面的边长。
ｉ
利用逐步等效线性 Ｊｏｈｎｓｏｎ求交法可求得各失效模式在标准正态空间中的线性化功能函数。若两
个失效模式线性化功能函数如下
) Ｔ ＝ ０
{ Ｇ（Ｕ） ＝ α １ Ｕ ＋ β １ （２２）
１
)
Ｔ
Ｇ（Ｕ） ＝ α ２ Ｕ ＋ β ２ ＝ ０
２
)
，
式中：Ｇ（Ｕ）为失效模式 １的线性化功能函数，α １ ＝ ［ α １１ α １２ ，…，α １ｎ ］为其一次项系数矩阵，β １ 为
１
)
，
其常数项；Ｇ（Ｕ）为失效模式 ２的线性化功能函数，α ２ ＝ ［ α ２１ α ２２ ，…，α ２ｎ ］为其一次项系数矩阵，
２
为其常数项。
β ２
则两个失效模式间的相关系数为 ［４２］
ｎ
Ｔ
ρ １２ α １ α ２ ∑ α １ｉ α ２ｉ （２３）
＝
＝
ｉ ＝１
针对重力坝各失效模式间的相关系数较小的特点，可采用窄界限法计算重力坝体系可靠度，具体
计算公式如下
４
— １ ８ １ —