Page 115 - 2023年第54卷第2期

表 ２ 西干渠取水流量和控制点目标水位设置
３
３
Ｑ１ ＝ ５０ｍ ?ｓ Ｑ２ ＝ ６５ｍ ?ｓ
渠池编号
３ ３
取水 Ｔ１?（ｍ ?ｓ） 水位 Ｌ１?ｍ 取水 Ｔ２?（ｍ ?ｓ） 水位 Ｌ２?ｍ
１ ２．１０ ３．２０ ２．８０ ３．５０
２ １２．００ ３．１０ １５．４０ ３．４０
３ ２．７０ ３．００ ３．６０ ３．３０
４ ３．６０ ３．００ ４．６０ ３．３０
５ ３．６０ ２．９０ ４．６０ ３．２０
６ ８．６０ ２．９０ １１．２０ ３．２０
７ ３．７０ ２．７０ ４．８０ ３．００
８ ４．１０ ２．５０ ５．４０ ２．８０
９ ３．２０ ２．４０ ４．２０ ２．７０
１０ ２．１０ ２．８０

５．３ 结果与讨论 因为 ＬＱ控制一般不考虑未来的扰动，故采用 ＩＤ模型，简记为 Ｉ － ＬＱ；ＡＰＣ控制需
要系统观测数据为支撑，必须采用 ＳＩＤ模型，简记为 Ｓ － ＡＰＣ；而 ＭＰＣ两种模型均可采用，分别记为
Ｉ － ＭＰＣ和 Ｓ － ＭＰＣ。本研究采用 ＳＯＢＥＫ模拟软件对西干渠运行情景进行仿真，用 ＭＡＴＬＡＢ进行控制算
法编程，控制时间间隔设置为 ５ｍｉｎ，预测时域设为 ６０，经反复试验，权重矩阵取 Ｒ ＝ ０．３ Ｑ时，控制
效果相对较好，结果讨论如下。
（１）系统模型比较。基于圣维南方程的非恒定
流模拟结果如图 ５所示。可以看到，靠下游渠池较
为明显地分为回水区与均匀流区两个分区，而靠上
游的渠池分区并不明显，这与前节对 ＩＤ模型的分
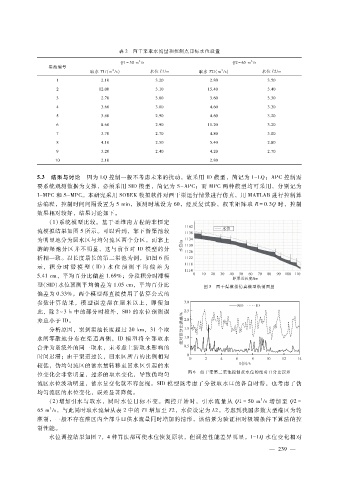
析相一致。以长度最长的第二渠池为例，如图 ６所
示，积 分 时 滞 模 型 （ＩＤ）水 位 预 测 平 均 偏 差 为
５．４１ｃｍ，平均百分比偏差 １．６９％；分段积分时滞模
型（ＳＩＤ）水位预测平均偏差为 １．０５ｃｍ，平均百分比
图 ５ 西干渠模拟仿真模型纵剖面图
偏差为 ０．３３％。两个模型都直接使用了估算公式的
参数计 算 结 果，模 型 误 差 都 在 厘 米 以 上，即 便 如
此，除 ２～３ｈ中的部分时段外，ＳＩＤ的水位预测误
差总小于 ＩＤ。
分析原因，案例渠池长度超过 ２０ｋｍ，３１个取
水闸零散地分布在渠道两侧，ＩＤ模型 将全 部取水
合并为系统外的同一取水，未考虑上游取水影响的
时间迟滞；由于渠道过长，回水区所占的比例相对
较低，伪均匀流区的蓄水量转移至回水区引起的水
图 ６ 西干渠第二渠池控制点水位的绝对百分比误差
位变化会非常明显，过多的取水变化，导致伪均匀
流区水位波动明显，蓄水量变化就不容忽视。ＳＩＤ模型既考虑了分散取水口的各自时滞，也考虑了伪
均匀流区的水位变化，误差显著降低。
３
（ ２）增加引水与取水，同时水位目标不变。调控开始时，引水 流量 从 Ｑ１ ＝ ５０ｍ ?ｓ增 加至 Ｑ２ ＝
３
６５ｍ ?ｓ，与此同时取水流量从表 ２中的 Ｔ１增加至 Ｔ２，水位设定为 Ｌ２。考虑到我国多数大型灌区为轮
灌制，一般不存在灌区内全部斗口供水流量同时增加的情形，该情景为验证相对极端条件下算法的控
制性能。
水位调控结果如图 ７，４种算法都可使水位恢复原状，但调控性能差异明显。Ｉ － ＬＱ水位变化相对

— ２ ３ ９ —