Page 114 - 2023年第54卷第2期

此，其流量过程属于控制变量 ｕ（ｋ）。在常水位调控模式下，系统的输出变量 ｙ（ｋ）即为 ９座节制闸的
闸前水位偏差。
表 １ 西干渠控制结构参数表

３
渠池编号 上游节制闸 渠池长度?ｍ 设计流量?（ｍ ?ｓ） 退水闸数量 直开口数量
１ 西干渠进水闸 ７４５０ ７１ ０ ７
２ 三棵树节制闸 ２０７８６ ６９ ３ ２８
３ 玉泉节制闸 １０３８７ ６１ ０ ９
４ 宁化节制闸 １７０９７ ５３ １ ８
５ 东一节制闸 １１６３０ ３５ １ ８
６ 平吉堡节制闸 １８２９７ ２７ ２ ２２
７ 镇北堡节制闸 ６２７３ ２２ １ ９
８ 白阳墩节制闸 ９９０２ １６ １ １２
９ 金山节制闸 ６６３５ １４ １ ９
１０ 暖泉节制闸 ４０６３ ８ １ ６

灌溉输配水自动控制的前提是被控闸门均具有流量、水位、开度的实时观测，并可远程、实时地
ｂ
控制开度。本研究根据理论公式估算一组回水区长度 Ｌ和动力波速 ｖ 的取值，基于该初始参数分别建
ｉ ｉ，ｊ
立 ＬＱ控制器、ＭＰＣ控制器和 ＡＰＣ控制器。ＬＱ控制器以式（６）建模、式（７）求解，为反馈控制，ＭＰＣ
和 ＡＰＣ控制器以式（１１）建模、式（１７）求解，为前馈反馈耦合控制，其中，ＬＱ和 ＭＰＣ属于定参数控
制器，运行过程中控制器参数保持不变，ＡＰＣ则随观测数据的更新，自动更新控制器参数。本案例的
ＡＰＣ控制器中，自适应控制采用差分进化算法 （ＤＥ），预测控制采用 径 向基 神 经 网络 （ＲａｄｉｃａｌＢａｓｉｓ
Ｆｕｎｃｔｉｏｎ ，ＲＢＦ）。
ＩＤ模型的参数估算方法可参见文献［２６］，ＳＩＤ模
型的回水区长度计算与之相同，但迟滞时间计算不同，
ＳＩＤ模型的分段处并无实体结构产生回波，动力波速采
用静水波速加水流流速，计算式如下：
Ｒ ｘ
ｉ ，ｊ
ｖ ＝ ｇＡ ?Ｂ ＋ Ｒ Ｄ （２９）
ｉ，ｊ 槡 ｉ，ｊ ｉ，ｊ ｎ ｉ，ｊ 槡 ｉ，ｊ ｉ，ｊ
２
式中：Ａ 为过流面积，ｍ ；Ｂ 为水面宽，ｍ；Ｒ 为水
ｉ，ｊ ｉ，ｊ ｉ，ｊ
力半径，ｍ；ｎ 为糙率；Ｄ 为底坡；ｘ为谢才 系数 中
ｉ，ｊ ｉ，ｊ
２
的指数参数；ｇ为重力加速度，ｍ?ｓ。西干渠自适应预
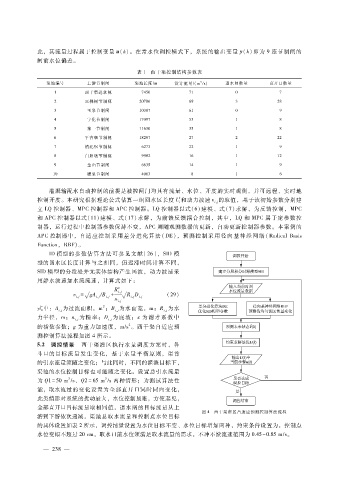
测控制算法流程如图 ４所示。
５．２ 调控情景 西干渠灌区执行水量调度方案时，各
斗口的目标流量发生变化，基于水量平衡原则，渠首
的引水流量须随之变化；与此同时，不同的灌溉目标下，
渠池的水位控制目标也可能随之变化。设置总引水流量
３
３
为 Ｑ１ ＝ ５０ｍ ?ｓ、Ｑ２ ＝ ６５ｍ ?ｓ两种情形；为测试算法性
能，取水流量的变化设置为全部直开口同时同向变化，
此类情形对系统的扰动最大，水位控制最难，方便起见，
全部直开口目标流量取相同值，退水闸的目标流量从上
图 ４ 西干渠灌区自适应预测控制算法流程
游到下游依次递减，渠池总取水流量和控制点水位目标
的具体设置如表 ２所示，调控情景设置为水位目标不变、水位目标增加两种，约束条件设置为，控制点
水位变幅不超过 ２０ｃｍ，取水口前水位须满足取水流量的需求，不冲不淤流速范围为 ０．４５～０．８５ｍ?ｓ。

— ２ ３ —
８