Page 20 - 2024年第55卷第9期
P. 20
但对高村、利津等站而言糙率值略有增加,且随流量增长基本接近常数。而河宽是与流量相关性较强
的因子,由图 1(f)可以看出河宽随糙率系数的变化趋势与流量极其相似,在以往的研究中通常是将河
宽与水深组成宽深比进行研究,或用单位宽度下的流量值作为计算条件求解水流阻力,因此无法单独
将河宽与水流阻力的变化联系起来。
3.3 组合参数对动床阻力影响分析 反映床面阻力影响的参数较多,根据前人研究选取弗劳德数 Fr =
[17 - 20] [35] [36 - 37]
V? gh 、宽深比 B?h 、河 道 纵 向 稳 定 系 数 D ?(hJ)、 相 对 粗 糙 度 k?h 、Shields数 Θ=
槡
s
50
- [4] [6] 为剪切应力,γ
50
τ c ?(( γ s γ )D ) 、沙粒剪切雷诺数 Re = U D ? ν 等无量纲参数进行比较,其中 τ c
50
为沙粒容重,U 为摩阻流速,ν 为运动黏滞系数。选用黄河下游花园口站实测资料,点
为水容重,γ s
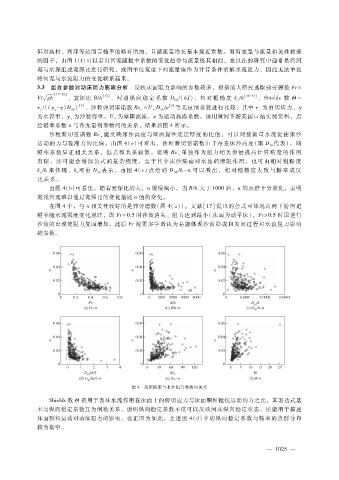
绘糙率系数 n与各无量纲参数间的关系,结果如图 4所示。
沙粒剪切雷诺数 Re 能反映床沙高度与壁面黏性底层厚度的比值,可以间接衡量水流促使床沙
运动的力与黏滞力的比值。由图 4(e)可看出,沙粒剪切雷诺数由于存在床沙高度(取 D 代表),同
50
糙率系数呈正相关关系,但点群关系较散,说明 Re 单独作为阻力相关参量提高 计 算 精 度 的 作 用
有限,还可能会增加公式的复杂程度,至于其中床沙肤面对水流的摩阻作用,也可由相对粗糙 度
k?h来体现,k可由 D 表示。由图 4(c)点 绘 的 D ?h - n可 以 看 出, 相 对 粗 糙 度 大 致 与 糙 率 成 反
s s 50 50
比关系。
由图 4(b)可看出,随着宽深比增大,n缓慢减小,当 B?h大于 1000后,n的点群十分散乱,表明
宽浅河流难以通过宽深比的变化描述 n值的变化。
在图 4中,与 n相关性较好的是弗劳德数(图 4(a))。文献[17]提出的公式可体现黄河下游河道
糙率随水流强度变化规律,即 Fr = 0.5 时沙波消失、阻力达到最小(床面为动平床),Fr>0.5时因逆行
沙波的出现使阻力复而增加,此后 Fr被更多学者认为是能体现沙波形成和发展过程对水流阻力影响
的参数。
图 4 动床糙率与水沙组合参数间关系
Shields数 Θ是用于表征水流作用在床面上的剪切应力与床面颗粒抵抗运动的力之比,其表达式基
本与纵向稳定系数互为倒数关系,说明纵向稳定系数不仅可以反映河床纵向稳定状态,还能用于描述
床面颗粒运动对动床阻力的影响,也正因为如此,上述图 4(d)中的纵向稳定系数与糙率的点群分布
较为集中。
0
— 1 2 5 —