Page 33 - 2021年第52卷第8期

相关性随着相隔时段的增加递减，短期径流预报序列 E 在不同时段间的预报误差 e 之间存在显著的
t
相关性。
由上述分析可知，不同时段预报误差 e 之间存在多种相关关系，因此本文采用 Student t copula 函
t
数建立各时段预报误差的联合分布，其能够较好的构建变量之间复杂的相关性特征。Student t copula
函数拟合参数及 K-S 检验结果见表 3。由表 3 可知，拟合结果可以通过假设检验。可以将其用于耦合
模型的求解中。
表 4 量级 3 下 Student t copula 函数拟合检验结果

df
θ 1 θ 2 θ 3 θ 4 θ 5 θ 6 p-value
0.67 0.52 0.39 0.78 0.65 0.84 5.00 0.94
5.2 短期运行结果分析 本文以 1 日为调度期长度，计算时段数为 24，各计算时段长为 1 h。量级 3
下，各时段径流预报误差 e 的统计特征均值均大于 0，这说明当预报的径流序列属于量级 3 时，实际
t
预报往往会高估实测径流，因此以 2018 年 10 月 17 日为典型日，其各时段预报径流值均高于实际径流
值，能够代表量级 3 下的预报径流序列特征。将典型日 4 时刻的预报径流数据插补延长为 24 时刻预报
径流数据，以调度期总发电量最大为目标，建立锦西水电站短期优化调度模型。为了更好的分析和
评价本研究所建模型的适用性与优势，本文分别建立传统的确定性优化模型（简称“确定性模型”）和
耦合整体预报不确定性的优化模型（简称“耦合模型”），同时采用实测径流序列根据确定性优化模型
制订“理想方案”，用于比较两种模型计算结果与理想方案之间的区别。
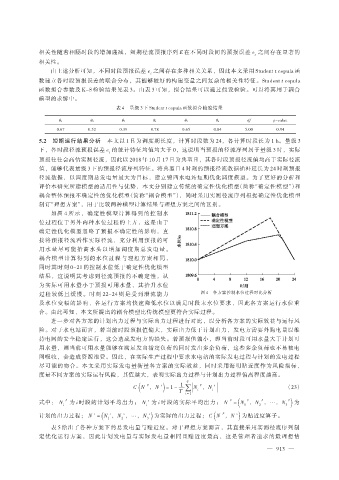
如图 4 所示，确定性模型计算得到的控制水
位过程位于另外两种水位过程的上方，这是由于
确定性优化模型忽略了预报不确定性的影响，直
接将预报径流看作实际径流，充分利用预报的可
用水量尽可能抬高水头以增加调度期总发电量。
耦合模型计算得到的水位过程与理想方案相同，
同时其时刻 0-21 的控制水位低于确定性优化模型
结果，这说明其考虑到径流预报的不确定性，认
为实际可用水量小于预报可用水量，其抬升水位
过程较低且缓慢。时刻 22-24 则是受到泄流能力 图 4 各方案控制水位过程对比分析
及水位变幅的影响，各运行方案均快速降低水位以满足时段末水位要求，因此各方案运行水位重
合。由此可知，本文所提出的耦合模型比传统模型更符合实际过程。
进一步对各方案的计划出力过程与实际出力过程进行对比，以分析各方案的实际效益与运行风
险。对于水电站而言，若当前时段预报值偏大，实际出力低于计划出力，发电方需要外购电量以维
持电网的安全稳定运行，这会造成发电方的损失。若预报值偏小，即当前时段可用水量大于计划可
用水量，则当前可用水量能够在满足发出指定负荷的同时发出多余负荷，这些多余负荷也不易被电
网吸收，会造成资源浪费。因此，在实际生产过程中要求水电站的实际发电过程与计划的发电过程
尽可能的吻合。本文采用实际发电量衡量各方案的实际效益，同时采用海明贴近度作为风险指标，
度量不同方案的实际运行风险，其值越大，表明实际出力过程与计划出力过程偏离程度越高。
T
(
p
p
C N ，N s ) = 1 - 1 å | | N ，N i s | | （23）
T
i
i = 1
(
p
p
式中： N i p 为 i 时段的计划平均出力； N i s 为 i 时段的实际平均出力； N p = N ，N ，，N 3 p ) 为
2
1
(
p
s
s
s
计划的出力过程； N = ( N ，N ，，N s ) 为实际的出力过程； C N ，N s ) 为贴近度算子。
1 2 3
表 5 给出了各种方案下的总发电量与贴近度。对于理想方案而言，其直接采用实测径流序列制
定优化运行方案，因此计划发电量与实际发电量相同且贴近度最高，这是管理者追求的最理想情
— 913 —